Cosmic ray exposure ages

Irradiation of bodies in space

Objects in space are constantly irradiated with high-energy particles. Two sources of such particles exist in the solar system: solar cosmic rays (SCRs) originating from the sun and galactic cosmic rays (GCRs).

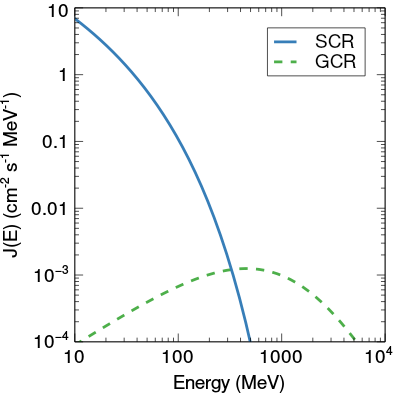
Above figure shows a comparison of the SCR (blue, solid line) and GCR (green, dashed line) spectrum. The SCR can only penetrate the upper few centimeters of any given material in space due to its low energies. On the other hand, GCRs can penetrate down to several meters below the surface of a given meteoroid. Since the outer layers of meteorites are generally lost, only the GCR flux matters when analyzing meteorites.

Note: Scientists working on cosmogenic nuclides generally distinguish between meteoroids and meteorites. A meteoroid is an rock in space that broke off from its parent asteroid, is thus irradiated by SCR and GCR, and has not hit the Earth yet. A meteorite on the other hand is the rock that fell from the sky, i.e., the meteoroid after it fell down to earth, thus passed the atmosphere and lost most of its outer material by ablation. This ablation usually leads to a meteoroid loosing its SCR record such that only GCR effects can be measured in meteorites.

Spallation reactions

The irradiation of material in space with high-energy particles induced the production of spallogenic nuclides. The figure below shows a schematic on how spallogenic reactions take place on the example of a ²⁸Si nucleus.

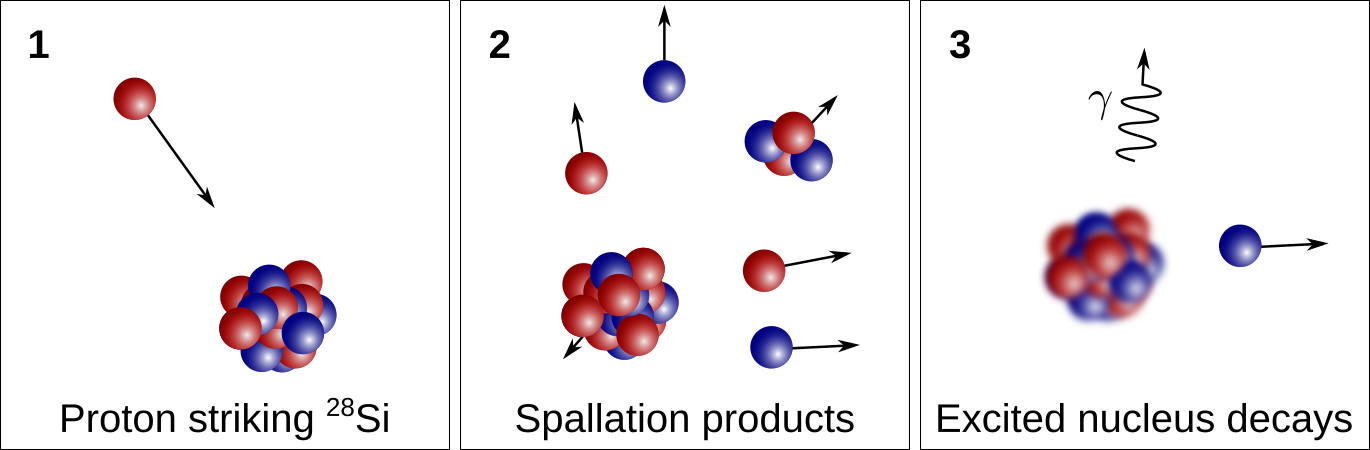
In panel (1), a high energy proton strikes a target nucleus (here ²⁸Si). This nucleus then breaks up into various lighter nuclei (2). The excited nucleus left behind then decays, e.g., via γ or neutron emission and a cosmogenic nuclide (here ²¹Ne) is left behind (3). For a given high-energy particle k (a proton for the example above) at a given energy E, the production of a cosmogenic nuclide j from a target element i can be calculated as:

$$P_{j,i,k} = \sigma_{j,i,k} J_k$$

Here, J_k describes the flux of the incident particle of a given energy. In a real scenario many target elements are present in a given meteoroid that can contribute to the production of nuclide j. Furthermore, the GCR and SCR have a variety of different energies, see for example the figure showing the SCR and GCR spectrum above. The total production rate P_j of nuclide j in a meteoroid can then be calculated as:

$$P_j = \sum_{i} c_i \frac{N_A}{A_i} \sum_k \int_0^{\infty} \sigma_{i,j,k} J_k(E)dE$$

The first sum over i considers the meteoroid’s composition. Here c_i is the concentration of target nuclide i, N_A Avogadro’s constant, and A_i the mean mass of nuclide i. The production rate also depends on different target elements k, to calculate the total production rate from all all projectiles we thus need to sum over k. The nuclear cross sections are of course projectile k, target nucleus i, product j, and energy E dependent, while the flux of the high-energy particles depends on their energy E. Integrating over all energies is thus required as well.

Cosmic ray exposure ages

The irradiation of a meteorite space induces spallation reactions and leads to the production of so called cosmogenic nuclides. Cosmogenic nuclide production is generally a very minor contribution and thus can only be detected in low-abundance isotopes, e.g., noble gases. If for example the ²¹Ne composition in a given meteorite can be measured (m) and the production rate P_j can be calculated, the time the object was irradiated in space can be determined as:

$$t = \frac{m}{P_j}$$

The time t is generally referred to as the cosmic ray exposure age of the sample. This technique has for example been used in order to determine the age of stardust grains in a recent study.